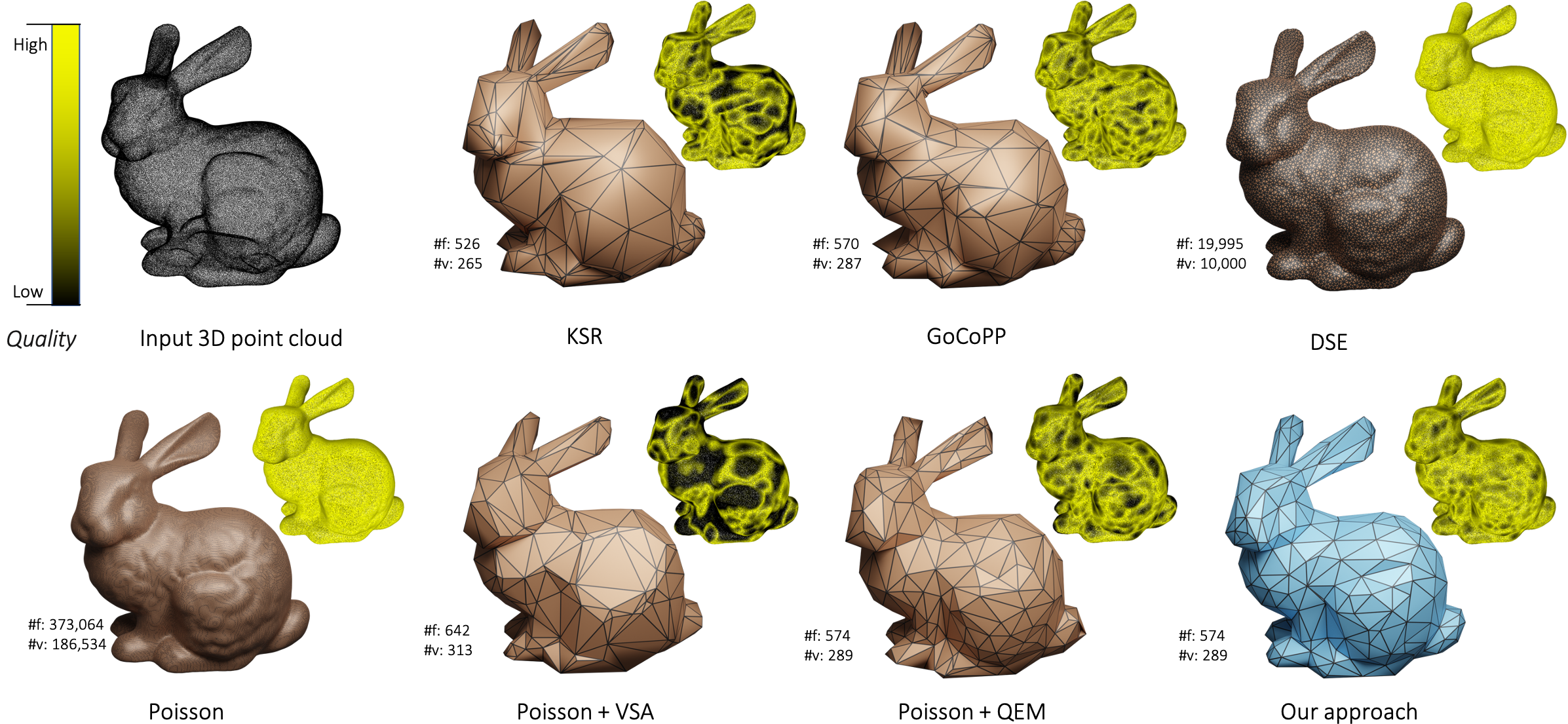
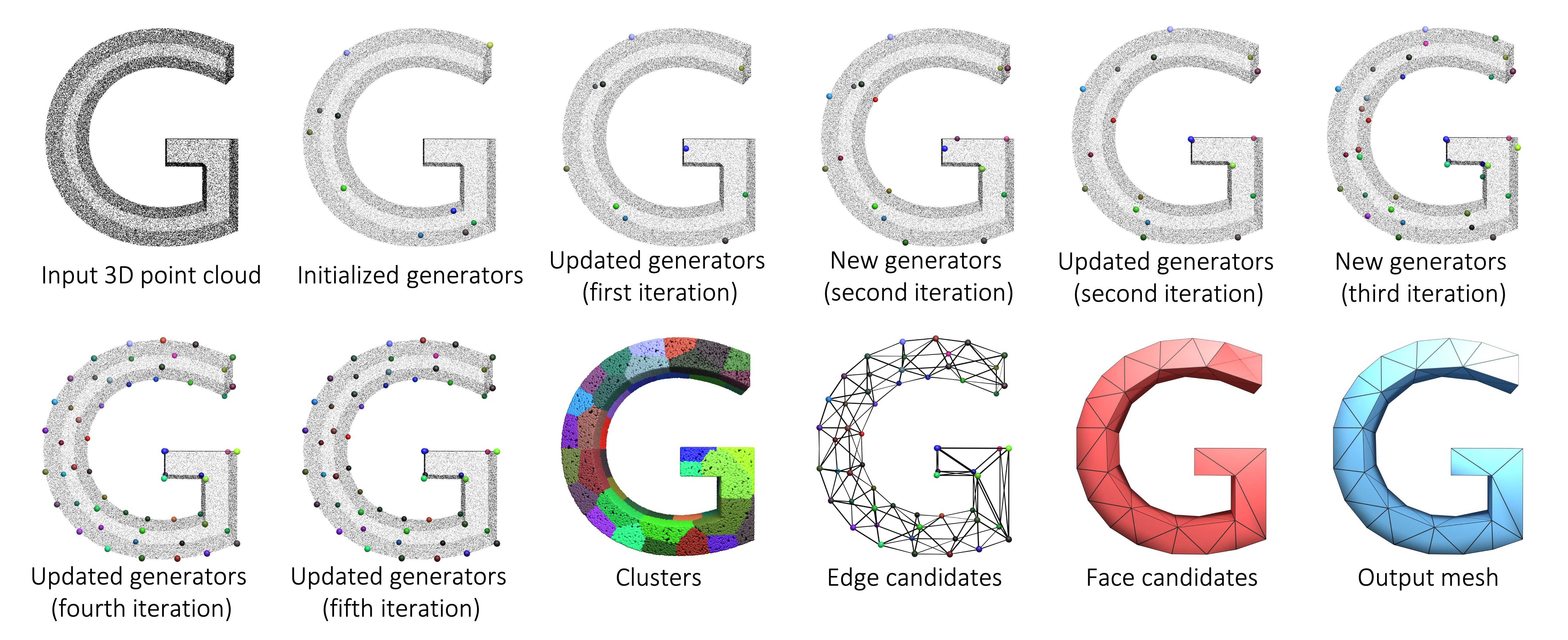BibTeX
@inproceedings{10.1145/3588432.3591529,
author = {Zhao, Tong and Bus\'{e}, Laurent and Cohen-Steiner, David and Boubekeur, Tamy and Thiery, Jean-Marc and Alliez, Pierre},
title = {Variational Shape Reconstruction via Quadric Error Metrics},
year = {2023},
isbn = {9798400701597},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA}, url = {https://doi.org/10.1145/3588432.3591529},
doi = {10.1145/3588432.3591529},
booktitle = {ACM SIGGRAPH 2023 Conference Proceedings},
articleno = {45},
numpages = {10},
location = {Los Angeles, CA, USA},
series = {SIGGRAPH '23}
}